[머신러닝] 선형회귀와 그의 변형들 : Simple, Multiple, polynomial, Ridge, Lasso Linear Regression

이번 글에서는 데이터 분석의 기초인 선형 회귀와 그의 변형들에 대해 알아보려고 합니다.
데이터 분석은 현대 사회에서 매우 중요한 역할을 하며, 그중에서도 선형 회귀는 가장 기본적이면서도 강력한 도구 중 하나입니다.

 

단순 선형 회귀 (Simple Linear Regression)

가장 기본적인 선형 회귀로, 한 개의 독립 변수와 한 개의 종속 변수 간의 관계를 분석합니다. 즉 하나의 X 값을 가지고 Y를 예측하는 것입니다. 예를 들어, 공부 시간과 시험 점수 사이의 관계를 알고 싶을 때 사용될 수 있습니다.

 

간단한 파이썬 코드 예시는 다음과 같습니다:

import numpy as np
from sklearn.linear_model import LinearRegression

# 데이터 생성
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 3.5, 3.8, 5, 7])

# 모델 훈련
model = LinearRegression()
model.fit(X, y)

# 결과 출력
slope = model.coef_[0]
intercept = model.intercept_
print(f"Simple Linear Regression Equation: y = {slope:.2f}x + {intercept:.2f}")

단순 선형 회귀. Simple Linear Regression

 

 

다중 선형 회귀 (Multiple Linear Regression)

 

여러 개의 독립 변수가 종속 변수에 영향을 주는 경우 사용됩니다. 즉 여러 개의 X 값을 가지고 Y를 예측하는 것입니다.

예를 들어, 집 가격을 예측할 때 방의 개수, 주변 시설 등 여러 변수가 영향을 미치게 됩니다.

 

코드 예시는 다음과 같습니다:

import numpy as np
from sklearn.linear_model import LinearRegression

# 데이터 생성
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]])
y = np.array([100, 150, 180, 200, 220])

# 모델 훈련
model = LinearRegression()
model.fit(X, y)

# 결과 출력
coefficients = model.coef_
intercept = model.intercept_
print(f"Multiple Linear Regression Equation: y = {coefficients[0]:.2f}x1 + {coefficients[1]:.2f}x2 + {intercept:.2f}")

 

Multiple Linear Regression. 다중 선형 회귀

이미지 출처 : https://corporatefinanceinstitute.com/resources/data-science/multiple-linear-regression/

 

 

다항식 회귀 (Polynomial Regression)

독립 변수와 종속 변수 간의 비선형적인 관계를 모델링할 때 사용됩니다. 선형이 아닌 데이터를 효과적으로 설명할 수 있습니다.  곡선의 다항식 선을 사용하고 과대적합이 나타나기 쉬습니다. X를 다항식으로 변경하여 모델링의 데이터로 사용합니다.

 

코드 예시는 다음과 같습니다:

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 데이터 생성
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2, 6, 8, 7, 5])

# 다항 특성 추가
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)

# 다항 회귀 모델 훈련
model = LinearRegression()
model.fit(X_poly, y)

# 결과 출력
print("Polynomial Regression Equation: y = ", end="")
for i, coef in enumerate(model.coef_):
    print(f"{coef:.2f}x^{i}", end=" ")
print(f"+ {model.intercept_:.2f}")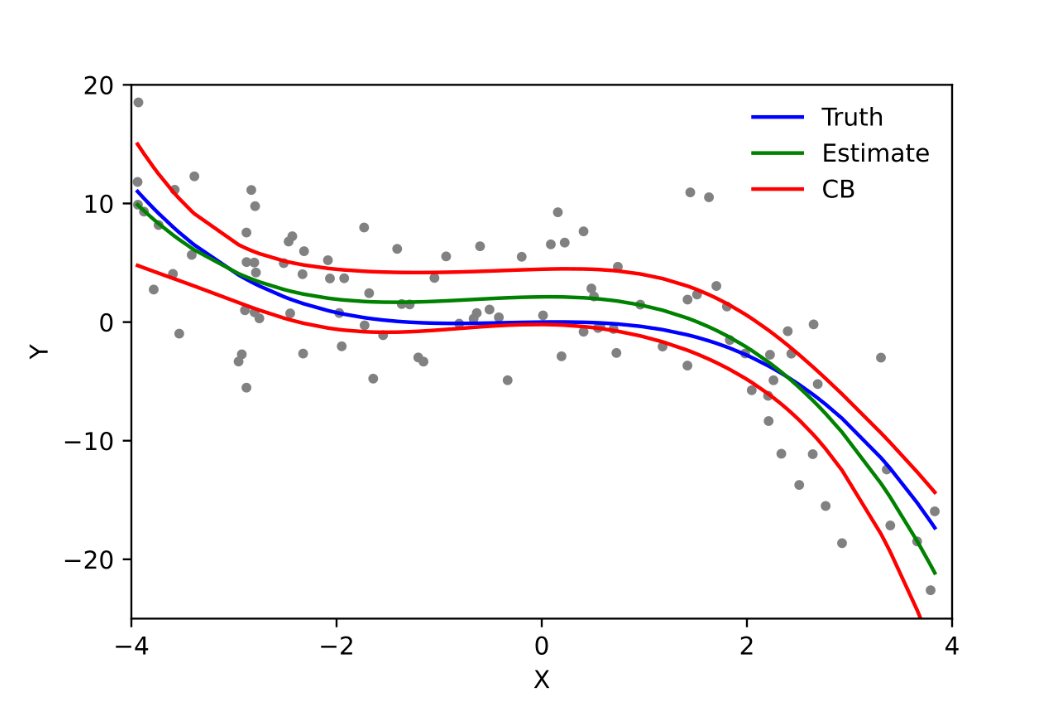

Polynomial Regression. 다항회귀

이미지 출처 : https://en.wikipedia.org/wiki/Polynomial_regression#/media/File:Polyreg_scheffe.svg

 

 

릿지(Ridge)와 라쏘(Lasso) 회귀

데이터가 다중 공선성을 가지거나 변수가 많을 때 사용되는 선형 회귀의 변형입니다. 과적합을 방지하고 모델의 일반화 성능을 높이는 데 도움이 됩니다.  독립변수들 간에 높은 상관관계가 있는 경우 규제화 (regularization)를 적용해 모델의 복잡도를 줄입니다.

 Ridge : 계수값을 0에 가깝게 만들지만 0 이 되지 않음.
 Lasso : 계수 값을 0 이 되게 함으로써 그에 해당하는 특성을 제외.

 

코드 예시는 다음과 같습니다:

import numpy as np
from sklearn.linear_model import Ridge, Lasso

# 데이터 생성
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2, 3.5, 3.8, 5, 7])

# 릿지 회귀
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X, y)

# 라쏘 회귀
lasso_model = Lasso(alpha=0.1)
lasso_model.fit(X, y)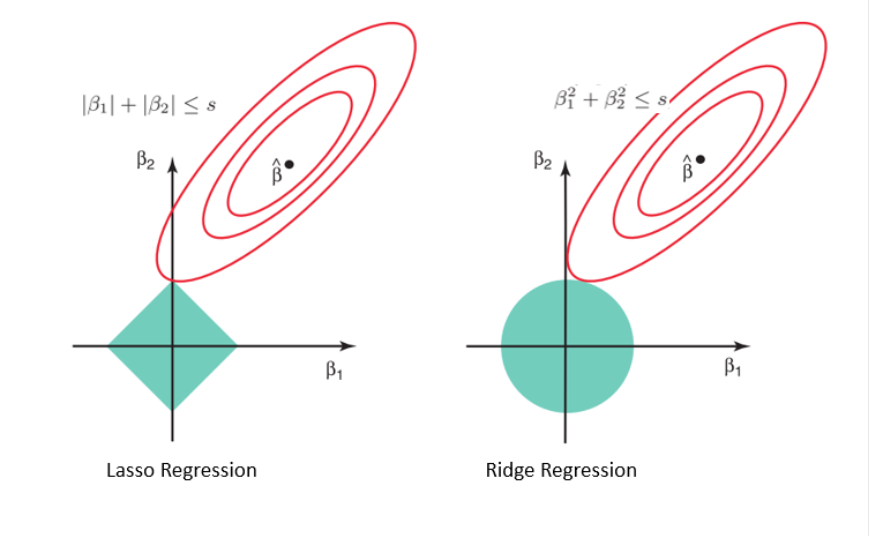

Ridge, Lasso regression. 릿지, 라쏘 회귀

이미지 출처 : https://www.datacamp.com/tutorial/tutorial-lasso-ridge-regression